| Issue |
ESAIM: Proc.
Volume 35, March 2012
Congrès National de Mathématiques Appliquées et Industrielles
|
|
|---|---|---|
| Page(s) | 114 - 121 | |
| DOI | https://doi.org/10.1051/proc/201235007 | |
| Published online | 06 April 2012 | |
Stabilité sous condition CFL non linéaire
1
Laboratoire de Mécanique, Modélisation & Procédés Propres
- UMR-6181 CNRS - IMT La Jetée, Technopôle de Château-Gombert,
38 rue Frédéric Joliot-Curie,
13451
Marseille Cedex 13, France
2
CERFACS, 42,
Avenue Gaspard Coriolis
31057 - Toulouse Cedex 01, France
We present a basic althought little known numerical stability condition: for convection
equations, the von Neumann stability constraint
∥un + 1∥L2 ≤ (1 + C Δt) ∥un∥L2
drives to the stability condition
Δt ≤ CΔxα
with
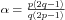 where p is an integer linked to the stability domain of the time scheme
and q ≥ p an integer linked to the upwind property of
the space discretization (in the centered case we have q = +∞ and
where p is an integer linked to the stability domain of the time scheme
and q ≥ p an integer linked to the upwind property of
the space discretization (in the centered case we have q = +∞ and
 ).
).
Résumé
Nous présentons une étude de stabilité aux conclusions originales : pour les équations de convection, la contrainte ∥un + 1∥L2 ≤ (1 + C Δt)∥un∥L2 fait apparaître la condition de stabilité Δt ≤ CΔxα avec
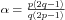 où p est un entier lié au domaine de stabilité du schéma en temps et q ≥ p un autre entier lié au caractère upwind de la discrétisation en espace (dans le cas centré, q = +∞). Des exemples numériques montrent la pertinence de cette étude.
où p est un entier lié au domaine de stabilité du schéma en temps et q ≥ p un autre entier lié au caractère upwind de la discrétisation en espace (dans le cas centré, q = +∞). Des exemples numériques montrent la pertinence de cette étude.
© EDP Sciences, SMAI 2012
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


