| Issue |
ESAIM: Proc.
Volume 26, 2009
Mathematical methods for imaging and inverse problems
|
|
|---|---|---|
| Page(s) | 24 - 44 | |
| DOI | https://doi.org/10.1051/proc/2009003 | |
| Published online | 25 April 2009 | |
Image processing by topological asymptotic analysis
Institut de Mathématiques de Toulouse, Université Paul Sabatier Toulouse 3, 31062 Toulouse cedex 9, France;
Corresponding author: auroux@math.univ-toulouse.fr
The aim of this article is to recall the applications of the topological asymptotic expansion to many image processing problems. We briefly review the topological asymptotic analysis. A very natural application of this technique in image processing is the inpainting problem, which can be solved by identifying the optimal localization of the missing edges. A second natural application is then the image restoration or enhancement problem. The identification of the main edges of the image allows us to preserve them, and to smooth the image outside the edges. We present then an application to the regularized and unsupervised classification problem. If the conductivity outside the edges goes to infinity, the regularized image is piecewise constant and provides a natural solution to the segmentation problem. We also mention that all these problems are solved with a  complexity. Finally, we present a hybrid scheme for contour detection and completion based on topological gradient and fast marching algorithms. We briefly illustrate all these applications with numerical results.
complexity. Finally, we present a hybrid scheme for contour detection and completion based on topological gradient and fast marching algorithms. We briefly illustrate all these applications with numerical results.
Résumé
Dans cet article, nous présentons l'application du gradient topologique à plusieurs problèmes classiques en traitement d'images. Après avoir brièvement introduit l'analyse asymptotique topologique, nous présentons son application naturelle au problème de l'inpainting, qui peut être résolu en identifiant la localisation optimale des contours manquants dans l'image. Une deuxième application naturelle est la restauration ou le débruitage d'images. L'identification des principaux contours permet de les préserver au cours du processus de restauration. Nous présentons ensuite une application à la classification régularisée et non supervisée. Lorsque la conductivité tend vers l'infini en dehors des contours, l'image régularisée devient constante par morceaux, et fournit une solution naturelle au problème de segmentation d'une image. Nous précisons ensuite la complexité de tous ces algorithmes, en 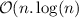 . Enfin, nous présentons un algorithme hybride pour la détection et fermeture des contours d'une image, basé sur les algorithmes du gradient topologique et des chemins minimaux. Pour chacune des applications, nous illustrons l'algorithme avec quelques résultats numériques.
. Enfin, nous présentons un algorithme hybride pour la détection et fermeture des contours d'une image, basé sur les algorithmes du gradient topologique et des chemins minimaux. Pour chacune des applications, nous illustrons l'algorithme avec quelques résultats numériques.
Mathematics Subject Classification: 68U10 / 94A08 / 41A58 / 35Jxx / 35Q80
Key words: Topological gradient / image processing / image inpainting / image restoration / image classification / image segmentation / minimal paths / asymptotic expansion.
© EDP Sciences, ESAIM, 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


